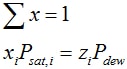Phase Equilibrium calculations

In the Ideal Thermodynamic example, only the vapor and liquid phases are provided. Only a single liquid phase is supported. The following flash specifications are supported:

• Temperature and pressure
• Temperature and vapor phase fraction
• Pressure and vapor phase fraction
• Pressure and enthalpy
• Pressure and entropy

As the vapor phase enthalpy does not depend on pressure, and none of the liquid phase properties depend on pressure, the T–h and T–s are not provided.
Vapor-liquid equilibria are calculated at given T and P from:

• The dew point pressure at given temperature follows from:
  F_V = 1, F_L = 0, y = z
  solve:

           solution:

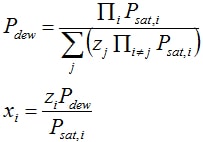
• Similarly, the bubble point follows from F_V = 0, F_L = 1, x = z and

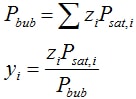
• For P > P_bub, the solution is a single phase liquid, with F_L = 1, x = z.
• For P < P_dew, the solution is a single phase vapor, with F_V = 1, y = z.
• For P_dew ≤ P ≤ P_bub the solution is two-phase. The solution follows from

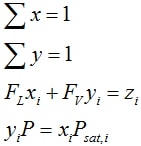
for x, y, F_L and F_V. The system is solved using a one dimensional solver to solve the Rachford Rice equation:

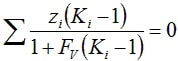
where the K values are given by Ki = φL/ φV  = P_sat,i/P and the vapor fraction F_V is solved for.

The T–F_V flash for F_V­ = 0 or F_V­ = 1 is solved as a dew- or bubble-point problem. For 0 < F_V­ < 1, a one dimensional problem is solved for which the pressure is adjusted so that the TP flash returns the desired vapor fraction.
Similarly, the P–F_V flash for F_V­ = 0 or F_V­ = 1 is solved as a dew- or bubble-point problem. For 0 < F_V­ < 1, a one dimensional problem is solved for which the temperature is adjusted so that the TP flash returns the desired vapor fraction.
The P–h and P–s, a one dimensional problem is solved for which the temperature is adjusted so that the TP flash returns a mixture with proper overall enthalpy or entropy.